逻辑回归介绍 ​

逻辑回归（Logistic Regression）是机器学习中的一种分类模型，逻辑回归是一种分类算法，虽然名字中带有回归，但是它与回归之间有一定的联系。由于算法的简单和高效，在实际中应用非常广泛。

1 逻辑回归的应用场景 ​

• 广告点击率
• 是否为垃圾邮件
• 是否患病
• 金融诈骗
• 虚假账号

看到上面的例子，我们可以发现其中的特点，那就是都属于两个类别之间的判断。逻辑回归就是解决二分类问题的利器。

2 逻辑回归的原理 ​

要想掌握逻辑回归，必须掌握两点：

• 逻辑回归的输入值。
• 逻辑回归的输出值。

2.1 输入 ​

逻辑回归的输入就是一个线性回归的结果。

2.2 激活函数 ​

• sigmoid函数

• 判断标准
  • sigmoid 函数接受回归的结果输入值。
  • 输出结果：[0, 1]区间中的一个概率值，默认为0.5为阈值。

逻辑回归最终的分类是通过属于某个类别的概率值来判断是否属于某个类别，并且这个类别默认标记为1(正例),另外的一个类别会标记为0(反例)。（方便损失计算）

输出结果解释：假设有两个类别A、B，并且假设我们的概率值为属于A(1)这个类别的概率值。现在有一个样本的输入到逻辑回归中得到输出结果0.6，那么这个概率值超过0.5，意味着我们训练或者预测的结果就是A(1)类别。那么反之，如果得出结果为0.3那么，训练或者预测结果就为B(0)类别。

对于如何衡量逻辑回归的误差，我们不使用前面线性回归的均方误差来很亮误差，而是使用下面的对数似然损失函数来衡量误差。

3 损失以及优化 ​

3.1 损失 ​

逻辑回归的损失，称之为对数似然损失，公式如下：

• 分开类别：

  $$\mathrm{cost}(h_{\theta }(x),y)=\{\begin{array}{ll}-\log (h_{\theta }(x))& \text{ if }\mathrm{y}=1\\ -\log (1-h_{\theta }(x))& \text{ if }\mathrm{y}=0\end{array}$$

  我们可以绘制上面的公式的图像来进行简单分析。

  

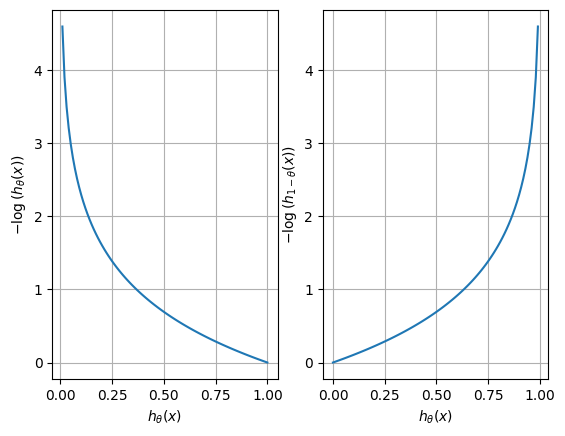
  当真实值为1时，预测概率值越接近于1，那么损失值越小。反之，当真实值为0时，预测概率值越接近于0，那么损失值越小。

• 综合完整损失函数

  $$\mathrm{cost}(h_{\theta }(x),y)=\sum _{i=1}^m-y_i\log (h_{\theta }(x))-(1-y_i)\log (1-h_{\theta }(x))$$

  这个式子和信息熵类似。

  接下来我们就带入上面那个例子来计算一遍。

  

  我们已经知道，log(P), P值越大，结果越小，所以我们可以对着这个损失的式子去分析

3.2 优化 ​

同样使用梯度下降优化算法，去减少损失函数的值。这样去更新逻辑回归前面对应算法的权重参数，提升原本属于各自类别的概率。