多层感知机
多层感知机在输出层和输入层之间增加一个或多个全连接隐藏层,并通过激活函数转换隐藏层的输出。
激活函数
激活函数(activation function)通过计算加权和并加上偏置来确定神经元是否应该被激活, 它们将输入信号转换为输出的可微运算。
一般来说,有了激活函数,就不可能再将我们的多层感知机退化成线性模型。
ReLU函数(修正线性单元):
导数:
sigmoid函数(S型函数):
导数:
tanh函数(双曲正切函数):
导数:
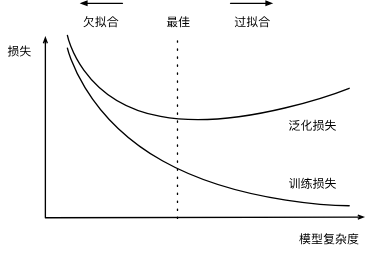
欠拟合和过拟合
权重衰退
限制特征的数量是缓解过拟合的一种常用技术。
在训练参数化机器学习模型时, 权重衰减(weight decay)是最广泛使用的正则化的技术之一, 它通常也被称为
使用
正则化是处理过拟合的常用方法:在训练集的损失函数中加入惩罚项,以降低学习到的模型的复杂度。
暂退法
深度网络的泛化性质令人费解,而这种泛化性质的数学基础仍然是悬而未决的研究问题。
暂退法在前向传播过程中,计算每一内部层的同时注入噪声,这已经成为训练神经网络的常用技术。
在标准暂退法正则化中,通过按保留(未丢弃)的节点的分数进行规范化来消除每一层的偏差。 换言之,每个中间活性值
通常,我们在测试时不用暂退法。 给定一个训练好的模型和一个新的样本,我们不会丢弃任何节点,因此不需要标准化。
暂退法在前向传播过程中,计算每一内部层的同时丢弃一些神经元。
暂退法可以避免过拟合,它通常与控制权重向量的维数和大小结合使用的。
暂退法仅在训练期间使用。
前向传播、反向传播、计算图
前向传播(forward propagation 或 forward pass):按顺序(从输入层到输出层)计算和存储神经网络中每层的结果。
反向传播(back-propagation):按相反的顺序(从输出层到输入层)计算和存储神经网络的中间变量和参数的梯度。
数值稳定性和模型初始化
梯度爆炸:参数更新过大,破坏了模型的稳定收敛。
梯度消失:参数更新过小,在每次更新时几乎不会移动,导致模型无法学习。
ReLU激活函数缓解了梯度消失问题,这样可以加速收敛。
环境和分布偏移
在许多情况下,训练集和测试集并不来自同一个分布。这就是所谓的分布偏移。
真实风险是从真实分布中抽取的所有数据的总体损失的预期。然而,这个数据总体通常是无法获得的。经验风险是训练数据的平均损失,用于近似真实风险。在实践中,我们进行经验风险最小化。
在相应的假设条件下,可以在测试时检测并纠正协变量偏移和标签偏移。在测试时,不考虑这种偏移可能会成为问题。
在某些情况下,环境可能会记住自动操作并以令人惊讶的方式做出响应。在构建模型时,我们必须考虑到这种可能性,并继续监控实时系统,并对我们的模型和环境以意想不到的方式纠缠在一起的可能性持开放态度。